从对称到超对称
- 作者:Julius Wess 译者:卢昌海 - 译者序: 2007 年 8 月 8 日, 每位学习超对称的物理系学生都知道的 Wess-Zumino 模型的提出者之一, 奥地利物理学家 Julius Wess 在德国汉堡去世, 享年 72 岁。 在 Wess 去世前不久, 他向 Proceedings of SUSY07 及 The European Physical Journal C 的 Supersymmetry at the dawn of the LHC 专刊提交了一篇带有回忆性质的介绍超对称概念发展的文章草稿, 题为 “From Symmetry to Supersymmetry”。 他的去世使那篇草稿成为了遗稿。 2009 年 2 月, 该遗稿在经过 I. Gebauer 和 P. M. Zerwas 的编辑之后得以发表, 这便是本文。 一般说来, 物理学家 - 尤其是在物理学史上曾占一席之地的物理学家 - 的晚年作品中最易流传的往往是回忆文章, 因为无论晚年物理学家在知识和观念上是否已经落伍, 他们作为亲历者的回忆都具有独特的史料价值。 对本文来说, 除史料价值外, 我们也可以通过它看到作为最早研究超对称的物理学家之一的 Wess 本人对超对称的叙述及理解。 |
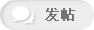
从一方面讲, 谈论对称性是很容易的。 每个人都有一个关于对称的观念, 从艺术到科学, 它是一个根基深厚且广为流传的观念。 每个人都能以这样那样的方式感受到对称性。 我认为值得一提的是, 大约三十年前, 人们曾以浓厚的兴趣对猿猴进行过实验, 看它们能学习多少东西。 其中的目标之一就是看猿猴如何学习画画。 在其中一个实验中, 纸的一边被画上了一个点, 猿猴会试图在另一边上画一个点来对称地平衡它。 那正是我们在物理学中所做的。 从另一方面讲, 谈论对称性是很困难的。 每个人, 包括物理学家, 对它都有着自己的观念, 你永远不会知道我们是否在谈论同样的东西。 幸运的是, 数学用它高超的抽象能力把对称性的观念抽象为了群的观念。 群论及群的表示论融合了我们在自然界、 艺术及科学等场合遇到的对称性的方方面面。 当我谈论对称性时, 我指的是群论、 群表示论、 代数及微分几何框架中的对称性。 在物理学上, 对称性自始至终都得到了应用。 群论方法使得从一个体系中获取信息变得大为容易。 一个象 Kepler 问题那样的问题如果不利用旋转对称性就会困难得多。 通过对称性你有可能无需真正理解支配一个体系的物理学定律, 或即便理解也无需能够求解动力学规律就能得到有关体系的信息。 你可以考虑一个平凡的例子: 天平。 基于对称性, 无需知道引力理论你就能相当确定天平左边和右边的物体具有相同的重量。 这示范了对称性如何在不知道规律的情况下帮助我们了解一个体系。 此外, 对称性通过守恒定律而与实验物理有着很强的相互关联。 能量、 动量和角动量的守恒可以通过实验来测量。 它们与时间平移、 空间平移及空间旋转下的不变性有关。 Noether 定理很准确地阐述了这一点: 如果我们知道一个体系在某种对称变换下不变, 我们就可以证明相应的守恒定律, 并且我们知道如何找到它的确切形式。 我们知道存在一个电荷守恒定律 - 我们需要一个对称性, 并在 Schrödinger 波函数的相位变化中找到了它。 这表明在数学抽象与实验事实间存在很强的联系。 我们很幸运地在物理学上拥有这种相互关联。 现代物理中的对称性甚至起着更强的作用, 以至于离开对称性的概念我们甚至无法表述现代物理学的定律。 为了使定域量子场论的框架有意义, 从一开始就必须考虑对称性。 我们不是在知道定律的情况下试图寻找对称性, 而是从一开始就必须贯彻对称性, 以便能以一种有意义的方式来表述那些定律。  | 图一. 粒子物理中的对称性 |
我准备了一幅列举某些基础对称性的图 (图一)。 它有两列: 左边的一列表示时空对称性, 右边的一列表示内部空间的对称性。 在左边那列的顶部我们有旋转对称群。 这是一个物理学家们可以用来学习群论的群。 我们知道静电学和静磁学定律都是在旋转群下不变的, Newton 定律也具有旋转不变性。 旋转群与二维特殊幺正群 SU(2) 有着密切关联, 而后者又与自旋的概念相联系。 你从量子力学中学到了所有这些。 当静电学和静磁学并入 Maxwell 的电磁学理论时, 我们遇到了 Lorentz 群。 尽管静电学和静磁学所描述的力在强度上相差光速的量级, 它们却同属一个理论 [译者注: “在强度上相差光速的量级” (different in strength by the order of magnitude of the velocity of light) 是一个不太恰当的说法, 其确切含义是指相差 v/c 或 (v/c)2 - 取决于如何比较 - 的量级]。 我们可以说这种统一来自于将旋转群推广为 Lorentz 群。 这是一个很好的模型, 让我们对理论如何能通过扩大一个群而得到统一有一个很好的理解。 右边那列显示了一个内部空间的对称性。 我曾经提到过波函数的相位变换。 波函数能够在更高维的空间 - 即我们称为内部空间的空间 - 中旋转。 这方面的第一步是由 Heisenberg 所做的。 他从旋转群及自旋的框架中学到了 SU(2) 是什么, 然后将这一概念作为同位旋用到了内部空间。 后来这又被推广到了 SU(3)。 这是一个我们如今通过夸克模型来理解的成功尝试。 一个非常成功的模型 - 粒子物理的标准模型 - 是基于一个描述色的 SU(3)C, 描述弱及电磁相互作用的 SU(2)W 及 U(1) 群。 Lorentz 群与这个 SU(3)C×SU(2)W×U(1) 一起构成了标准模型的基础。 如我们在实验室中所知, 这一模型很好地描述着直到 10-16 厘米尺度上的物理学。 我们很自然地想知道 SU(3)C×SU(2)W×U(1) 是否是一个更大的群 - 比如 SU(5) - 的一部分。 这可以导致强、 弱及电磁相互作用真正统一的理论。 这种理论我们称之为 GUT - 大统一理论, 但我们还不清楚大自然是否知道这一点。 建立在 Lorentz 群及 SU(3)C×SU(2)W×U(1) 群之上的标准模型才是迄今受到实验支持及很好检验的理论。 从这两列上看, 大自然 (或我们) 似乎将同样的对称性概念使用了两遍。 但大自然是分开选择了它们吗? 大自然是将同一件事情做了两遍吗? 我们很自然地想在这两列之间寻找桥梁。 我们从 Maxwell 方程组中学到变换参数可以选得与时空有关。 这是 Maxwell 理论的规范变换性质。 我们可以将 Maxwell 理论中的这一参数与 Schrödinger 波函数的相位变换的参数等同起来, 从而构筑出一个我们如今所说的规范理论。 这样规范理论的想法就诞生了。 你要求理论必须在一个作用于内部空间, 但参数与时空相关的群作用下不变。 这便是标准模型赖以建立的概念。 标准模型是 SU(3)C×SU(2)W×U(1) 群的规范理论。 如果把同样的规范概念用于时空对称性, 我们得到的是 Einstein 的引力理论。 我们知道标准模型 - 通过重整化的概念 - 可以被诠释为量子场论, 作为这样的理论, 它在短距离 - 我前面所说的 10-16 厘米的尺度 - 上获得了极大的实验成功。 我们会乐意通过从实验上发现对标准模型的偏离来得到下一步该如何走的启示: SU(3)C×SU(2)W×U(1) 似乎是我们所能作的最简单的选择, 它成功了, 所有的实验一次又一次地验证了它。 大自然是否就不比这更复杂了? 它难道不知道大统一? 至于 Einstein 的引力理论, 我们知道它在大尺度下是非常好的理论。 在那里我们没有理由怀疑它的有效性。 我们对大尺度下时空的理解就是基于这一理论。 我们的局面是: 标准模型与 Einstein 的引力理论很好地描述了来自实验室及天文和天体物理的观测数据。 甚至连基于这两个理论的宇宙学也很合理。 从我们的两列中, 现在我们看到了一个更令人困惑的局面。 同样的对称性及对之进行规范的概念在左侧给出了一个非常好的经典引力理论, 它通过大量的奇异性抗拒着量子化 [译者注: Wess 所用的部分术语不太规范, 比如此处用 “奇异性” (singularity) 来表示人们通常所说的 “发散性” (divergence)。 这一用法他在后文还将重复, 我们一律照原文进行翻译。]。 在经典引力理论与量子场论间似乎存在着一种深刻的冲突。 另一方面, 同样的对称性及对之进行规范的概念在右侧导致了一个数学上和实验上都非常成功的可重整量子场论模型。
从对称到超对称 (中) - 作者:Julius Wess 译者:卢昌海 - 规范就是全部呢, 还是存在着时空及内部空间对称性之间更加深刻的关联? 在核物理中, 很久以前 Wigner 和 Hund 提出过一个以自旋 SU(2) 及同位旋 SU(2) 为子群的 SU(4) 群。 通过这种方式他们统一了时空及内部空间, 并且得到了有关核能级的很好的分类。 当粒子物理用到了 SU(3) 时, 这一想法被推广为了 SU(6), 以包含自旋的 SU(2) 及内部空间的 SU(3)。 在 SU(6) 的基础上可以对带不同自旋 - 自旋 0 和 1 及自旋 1/2 和 3/2 - 的粒子的质量给予合理的实验预言 [译者注: SU(6) 并不是一个成功的模型, 它对粒子质量的预言其实并不比完全不假定跨自旋或跨 “味” 的对称性来得高明。]。 如今这已在夸克模型的基础上得到了更好的理解。 由于那时侯夸克模型尚不为人知, 人们曾做过很多尝试, 试图将 SU(6) 模型推广至包含 Lorentz 群。 但这被证实为是不可能的, 即不可能构筑一个在低能下具有 SU(4) 或 SU(6) 对称性的 Lorentz 不变的模型。 如果很多物理学家尝试了某件事情却没有成功, 那么聪明的做法也许是去试图证明那件事情是不可能成功的。 这正是人们所做的, 它以 O'Raifeartaigh 的工作为起始, 最终得到了一个如今被称为 Coleman-Mandula 此路不通定理 (no-go theorem) 的优美表述 [译者注: SU(4) 和 SU(6) 对称性的提出时间分别为 1937 年和 1964 年 (后者与夸克模型同年), O'Raifeartaigh 的工作发表于 1965 年, Coleman-Mandula no-go 定理则发表于 1967 年。]。 这个定理告诉我们, 对于一个以 Lorentz 群为对称群, 且满足我很快将会告诉你们的若干公理的四维时空中的理论, 对称群的唯一可能性就是 Lorentz 群与某些紧致内部群的直积。 我们居然有一个建立在很基本的公理基础上的定理来区分那两列, 这是足够奇怪的。 现在让我们来谈谈公理。 除 Lorentz 不变性外, 那些公理规定理论必须基于量子力学并且是局域的, 它必须是一个局域量子场论。 在这里局域指的是微观意义上的局域, 即两个类空分隔的观测 - 无论距离多近 - 不能彼此影响。 理论的局域性来自于场的局域性。 此外我们还假设存在一个唯一的能量最低态 - 一个我们称之为真空的基态, 所有其它态都具有更大的能量。 几率被假定为是在量子力学意义上守恒的。 最后, 我们假定只存在有限数目的不同粒子 [译者注: Wess 对最后这一假设的表述并不确切, 确切的表述是: 在任意一个给定的能标以下, 只存在有限数目的不同粒子。]。 这些看上去全都是很合理的假设, 但它们的推论之一就是你不能如我们试图通过假设一个 SU(4) 或 SU(6) 对称性所做的那样将两列合并起来。 这组公理有一个问题: 除自由场理论外, 我们还不知道任何一个其存在性能被严格证明, 并且满足所有公理的局域量子场论。 我们已经在微扰理论中发明了很有力的方法, 通过重整化手段分离无穷大。 我们能够用这种方法提取出可在实验上检验的信息。 从某种意义上讲, 这只是一种技巧, 但它工作得非常漂亮。 在这样的基础上我们理解着我所讨论的那些模型, 并使它们取得了成功。 然而这是一种数学家们不会乐意接受为理论的模型表述。 不过它与实验数据的比较是如此成功, 使得我们无法抛弃这种类型的理论。 现在我愿意提出一个观点。 假如我们想在前面讨论过的框架下构筑一个理论, 我们想要有自旋 0、 1 以及 1/2 的场。 我们从自由场出发, 试图通过调节多重态及耦合常数来使微扰理论中只出现有限数目的发散。 我们从树图开始, 研究 Feynman 图对能量动量的依赖性, 并调节模型使这种依赖性尽可能光滑, 以便为一圈图层次上对能量动量变量的积分创造便利。 这样做的结果是一个带有对称性自发破缺的规范理论。 因此, 即便不知道群论与对称性, 一个好的物理学家仍能在动力学的基础上发明规范理论的全部观念。 这一点在二十年前就已经由 Cornwell、 Llewellyn Smith 以及 Steve Weinberg 所阐明。 他们率先采用了这种方法。 在你知道了这一结果后, 通过一本群论教材, 将你的模型用你的群论知识表述出来, 并将对称群规范化, 就容易多了。 用这种方法你得到一个模型, 你会发现它是一个可重整的量子场论。 这可以由规范不变性得到证明。 Noether 定理及流的守恒是这一证明的核心。 流必须是一个具有良好定义的东西, 它有助于将无穷大以及未定义的常数联系起来, 使得最终出现的只是有限的数字。 这确定了重整化方案。 当我说即便表述一个物理理论也必须用到对称性的概念时, 我指的就是这个。 但这也提出了一个问题, 即对称性是真正基本的呢, 还是能在一些合理的公理基础之上从体系的动力学中推导出来? 我们的思维方式受深刻而广泛的对称性观念的影响是如此之大, 以至于如果我们在一个动力学体系中发现了一个漂亮的对称性, 我们就说我们理解了这个体系。 如果偏离了对称性, 我们则说: 一定有什么东西我们还没有理解。 由对称性而非动力学的需要出发还有一个很好的理由, 那就是后一种方法将会是困难的, 并且 - 依我说 - 也是丑陋的。 数学家们未曾从这种晦涩的途径出发来发展概念, 因而我们也没有能够使用的数学工具。 这与前一种方法相反, 在那里我们有各种各样漂亮的数学。 有一种联合时空对称性与内部对称性的令人惊讶的方法, 那就是通过超对称。 这是通过推广对称性的概念而达成的。 如你所知, 对称性可以用对易关系来表述, 就象量子力学中的角动量对易关系一样。 一大类群 - 李群 - 是与由对易关系所定义的李代数有关的。 我们已经提到过的所有对称性都是这种类型的。  | 图二 |
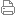
从 Dirac 那里我们知道: 不仅对易子, 而且反对易子也是非常有用的概念, 特别是当我们处理带半整数自旋的粒子时。 我们的想法是将对称性的概念推广为一种同时建立在对易子和反对易子之上的结构。 这在数学上并不是一种新的想法, 这样的结构 - 分级李代数 (graded Lie algebras) - 已经被彻底研究过了, 比如被 Berezin。 但是这样的一种概念能够在量子场论中实现吗? 答案是肯定的: 存在一种相当唯一的对称性, 它的唯一性是建立在 Coleman 和 Mandula 的此路不通定理基础之上的 (图二)。 这是由 Haag、 Lopuszanski 以及 Sohnius 所证明的。 在这里该定理并未说此路不通, 而是告诉你一条由下面这个公式所表示的非常唯一的道路 [译者注: 原文将 {QαN, QβM}+ 写成了 {QαN, QαM}+, 显系笔误。]: {QαN, QβM}+ = 2γαβνPνδNM | (1) |
荷 QαN 是旋量荷, α 是旋量指标, QαN 是 Majorana 旋量。 N 是一个自由指标。 如果 N 取值为从 1 到 2, 我们谈论的就是 N=2 的超对称。 如果它取值为从 1 到 4, 我们谈论的就是 N=4 的超对称。 四维矢量 Pν 是产生时空平移的能量动量四维矢。 这一代数的结构常数是 Dirac γ 矩阵与 Kronecker 符号。 这一代数可以与 Lorentz 群合并, 这样得到的就是超对称的代数。 这些荷现在可以通过局域场来实现, 超对称的代数关系在场的正则对易关系的基础上得以成立。 这些荷与流联系在一起, 那是 3/2 流, 就如同能量动量是与作为自旋 2 客体的能量动量密度张量联系在一起的。 如果理论被规范化, 那种流就是场的源 - 对于电流来说那是光子, 自旋为 1; 对于能量动量张量来说那是引力子, 自旋为 2; 对于超对称流 (supercurrent) 来说则是引力微子 (gravitino), 自旋为 3/2。 超对称理论有一个很令人鼓舞的特性: 作为量子场论, 它们要比没有超对称时具有更少的发散性。 超对称理论也有一个很不令人鼓舞的特性, 它是代数的直接推论, 那就是一个超对称理论必须具有相同数目且质量简并的玻色与费米自由度。 自然界并不是这样的。 我们有费米子和玻色子, 但并不存在于同一个多重态结构之内, 质量也并不简并。 这两个特性导致了困扰, 而且这困扰由于它们并非彼此独立而更严重。 让我用一个简单的例子来说明这一点。 考虑一个具有相同频率的玻色和费米谐振子, 它们的零点能具有相反的符号, 把它们加起来就会导致零点能的相互抵消。 一个场可以被看成是无穷多个谐振子之和, 其零点能的总和将是一个无穷大的真空能, 除非是在一个玻色子和费米子的贡献相互抵消的理论中。 Pauli 就已经知道了这一点, 但他同时也知道世界并不是这样的。 超对称将这种相互抵消与理论的代数结构联系在一起, 受此影响, 你也许会相信它已经建立在了有关理论与自然的一种更深刻的性质之上。 自 Pauli 时代以来, 我们已经学会了处理自发破缺的对称性。 在这种带有对称性自发破缺的理论中场论性质得到了维持, 但在低能唯象的层次上, 对称性看起来被显著的效应所破坏。 导致真空能抵消的这同一种机制还会导致很多其它发散性的抵消。 理论的这种得到改善的重整化性质可以归结到带有玻色或费米内线的图的抵消性质之上。 可以证明, 理论中的某些参数将不会有辐射修正, 甚至连有限的修正都没有。 这在量子场论中即便不是奇迹, 也是令人兴奋的。 你可以在非量子化的层次上引进诸如特定的质量或耦合常数之类的参数, 使之完全不受辐射修正。 很自然地, 这对基于超对称理论的粒子唯象学是有影响的。
从对称到超对称 (下) - 作者:Julius Wess 译者:卢昌海 - 让我首先讨论一下超对称理论具有相同数目的玻色子与费米子这一事实 [译者注: 这里实际指的是相同数目的玻色与费米自由度]。 我们知道在自然界中夸克与轻子是费米子。 这些是构成物质的粒子。 这些费米子每种都有两个玻色伙伴, 因为每个自旋 1/2 的粒子都有两个自由度。 我们不知道自然界中是否存在那样的伙伴, 但我们可以给它们命名。 我们把夸克的超对称伙伴称为 squark, 把轻子的超对称伙伴称为 slepton, 其中 "s" 指超对称伙伴的标量性 [译者注: 不知 squark 和 slepton 是否已有标准译名, 若没有的话, 建议译为标量夸克与标量轻子]。 我们知道在自然界中光子、 弱相互作用矢量粒子、 胶子、 引力子与 Higgs 粒子是玻色子。 这些是传递相互作用的粒子。 这些玻色子每种都必须有一个费米子伙伴。 我们给它们的命名为: photino、 wino、 zino、 gluino、 gravitino 和 Higgsino [译者注: 这其中 photino 和 gravitino 通常译为光微子和引力微子。 其余几种不知是否已有标准译名, 若没有的话, 建议译为 W 微子、 Z 微子、 胶微子和 Higgs 微子]。 图三. QCD 中的超对称顶点 [译者注: 此处 QCD 显系 QED 之笔误] 我们可以用这些粒子来构筑模型, 并把我们已经知道这类模型中一半的粒子当成是一种成功。 不仅如此, 我们还知道它们的耦合, 那是完全由我们已知的粒子的耦合所确定的。 选一个由已知粒子组成的费曼图 (图三), 这种图中那些要么从入射粒子到出射粒子, 要么形成圈的线, 能够并且必须出现在一个等价图中, 在那里它被对应于超对称伙伴的线所取代。 对所有的线作这样的替换, 你就可以得到一个特定超对称理论的所有的图。 那些相应顶点上的耦合常数与你作为出发点的理论中的相同。 在一个真正超对称的理论中, 质量也必须是相同的。 如果对称性自发破缺, 这一点就不成立。 我们知道在规范对称性的自发破缺中, 一个多重态中的质量差有可能很大 - 就象光子与 W 或 Z 粒子的质量差。 超对称也有可能通过这样的方式破缺, 以维持其重整化性质。 超对称伙伴的质量差有可能很大, 我们称其为超对称隙 (SUSY gap) 不过, 辐射修正将不会完全抵消 - 我们可以预期与超对称隙具有相同量级的有限贡献。 在具有这种性质的规范理论的质量与耦合常数中, 包含了 Higgs 质量及 Higgs 耦合常数。 知道了这一性质, 人们就可以将之与粒子理论中的另一个现象联系起来。 假设存在一个大统一理论, 大统一规范群必须自发破缺以产生我们所知道的标准模型。 而标准模型的对称群 SU(3)C×SU(2)W×U(1) 则破缺为如我们在低能区所知的电磁与弱相互作用理论 [译者注: 此处 “电磁与弱相互作用理论” 似应为 “电磁与强相互作用理论”, 后者才对应于标准模型中的非破缺部分]。 在量子场论模型中, 这一对称性破缺是由参数 - 即 Higgs 质量及 Higgs 耦合常数 - 引发的, 这些参数在非超对称理论中必须经受无穷大量的重整。 在这种破缺方案中, 很难理解两个不同能区的破缺如何能保持稳定并遵守能标。 这是粒子物理中的等级问题 (hierarchy problem)。 但假如理论是一个自发破缺的超对称理论, 那么有关参数只会受到的量级为超对称隙的辐射修正。 假如超对称隙是在表征 W 粒子质量的电弱破缺能标的量级上, 我们就能理解大统一理论中对称性破缺的稳定性。 在这样的方案中, 超对称隙必须在 TeV 量级上, 这是一个很快就会被实验所触及的能标。 我个人的信念是: 象超对称这样优美的对称性如果只是用来解决等级问题, 那将是巨大的浪费。 超对称在高能下也许扮演着重要得多的角色, 而解决等级问题只是它在低能下的残留之一。 不过请允许我强调, 这一预想有两个前提: 超对称与大统一。 它们的任何组合都有可能是对的或错的。  | 图四. 无重整性 |
现在回到在规范理论框架中就曾提到过的话题。 我们看到, 超对称在重整化理论的框架中对量子场论的动力学行为有很强的影响。 我们可以从这一框架出发, 寻找一个包含自旋 0 和 1/2, 不仅在树图而且在单圈图层次上都尽可能光滑的模型。 我们可以寻求无穷大真空能的抵消, 通过这种方式我们可以确立相同的玻色与费米自由度。 如果还要求我在前面谈及过的无重整性质, 我们就可以构造出有可能带有所谓软破缺 - 一种不影响重整化性质的对称性破缺 - 的超对称理论。 如果我们要求所有的辐射修正都消失, 我们将得到严格的超对称理论。 因此导致超对称的也同样可以是一个动力学概念, 只不过是被推进到了单圈图的层次上。 一个知道如何处理费曼图的好的物理学家, 有可能无需知道任何代数、 群或分级群, 就发现超对称。 从某种意义上讲, 超对称是可重整量子场论框架内继规范理论之后的下一个逻辑步骤。 从对应于经典理论的树图层次到由单圈图表示的量子层次, 将同样的观念重复用一次, 你就得到超对称。 我们所不知道的, 是大自然是否知道这种思考方式, 或者它有不同的逻辑, 以不同的方式做事情。 现在谈谈超对称的历史。 它始于 Golfand 和 Likhtman 的工作。 他们考虑了通过在 Poincare 代数中添加旋量生成元, 以扩展代数。 那大约是在 1970 年, 他们的确是在超对称的轨道上。 我将在此次讲演结束时回到这个想法上来, 因为我认为这是一个正确的问题, 即我们能否通过新的代数概念来扩展代数及对称性概念, 以得到新的对称性? 然后是 1972 年, Volkov 和 Akulov 在一篇文章中沿下列思路进行了思考: 我们知道对称性的自发破缺伴随有无质量的 Goldstone 粒子。 在自然界中我们知道一种质量 - 如果有的话 - 很小的自旋 1/2 粒子, 即中微子。 这种费米子有可能是某种对称性破缺的 Goldstone 粒子吗? Volkov 和 Akulov 构造了一个超对称的非线性拉氏量。 当然, 如今我们从 Haag、 Lopuszanski 及 Sohnius 知道那必须是超对称的[译者注: 这里提到的 “Haag、 Lopuszanski 及 Sohnius” 指的是所谓的 Haag–Lopuszanski–Sohnius 定理, 它表明一个四维时空量子场论所具有的最普遍的对称性是超对称, 并且其中的费米生成元具有 1/2 自旋。 这一定理被视为是 Coleman-Mandula 定理的推广]。 但由于是非线性的, 就象非线性 σ 模型, 那个拉氏量是高度不可重整的, 而且不具有任何我们如今在超对称中找到的有用及迷人的重整化性质的任何迹象。 通往超对称的另一条途径来自二维对偶模型。 Neveu 和 Schwarz 等人构筑了一个模型, 其中存在与超规范变换有关的旋量流, 它将标量场变换为旋量场。 不过, 这种变换的代数只在质壳上闭合。 该旋量流被称为超对称流, 那是 “超对称” 这一名称的由来。 1973 年, Bruno Zumino 和我发表了一篇文章, 在其中我们确立了四维的超对称, 构造了可重整的拉氏量, 并在单圈图层次上展示了无重整性质。 我们的出发点是超对称流及对 Noether 定理的很强的信心。 通过微扰量子场论的无重整性质推出超对称的文章则从未有人写过。 通过超对称可以很自然地将时空概念推广为超空间 (superspace) 的概念。 能量动量产生四维时空中的平移, 因此很自然地可以由反对易的荷在某个反对易的空间中产生某种平移。 这种新的空间与四维的 Minkowski 空间一起被称为超空间。 | 自旋 | 0 | 1/2 | 1 | 3/2 | 2 | | | | 2 | 1 | | | | Φ - 标量多重态 | | | | 1 | 1 | | | V - 矢量多重态 | | | | | | 1 | 1 | 引力多重态 |
表一 现在场变成了超空间变量的函数, 他们以一种很自然的方式包含了超对称多重态。 这一想法最初是由 Salam 和 Strathdee 提出的。 拉氏量可以很优美地用超场 (superfield) 来表述, 而无重整定理 (non-renormalization theorem) - 如 Fujikawa 和 Lang 所率先展示的 - 也得到了很优美的表述。 自旋 0 和自旋 1/2 的多重态在所谓的手征超场 (chiral superfield) 中找到了位置, 而自旋 1 和自旋 1/2 则出现在所谓的矢量超场 (vector superfield) 中 (见表一)。 由超场表示的任何只含手征场外线, 而不含共轭手征场 Φ* 或矢量场的图都不会被重整 (图四)。 在只含手征场的类别中若没有外场, 我们就得到关于真空能的无重整定理。 对超场拉氏量 L = Φ†egVΦ + m2Φ2 + λΦ3 | (2) |
的浏览告诉我们, 手征场的质量项具有 Φ2 的形式, 而 Higgs 类型的耦合项具有 Φ3 的形式。 这些耦合不会被重整。 手征场的动力学项形如 Φ*Φ, 则具有波函数重整。 超空间变量在我们要对超对称理论的内部对称性进行规范时, 也扮演着重要角色。 规范一个内部对称性意味着表述一个在参数与时空有关的变换之下不变的理论。 时空本身并不是一个超对称的概念, 我们必须将它换成超空间。 规范一个超对称理论中的内部对称性意味着表述一个在参数与超空间有关的变换之下不变的理论。 用这种方法我们明白了如何将所有的规范理论超对称化。 超对称的规范也在超空间中找到了自然的表述。 Einstein 的引力理论可以表述为四维时空中的几何理论。 超引力 - 具有规范化超对称的理论 - 可以表述为超空间中的几何理论。 超引力包含了 Einstein 的理论, 因为超对称包含了 Lorentz 群。 它改善了普通引力理论的重整化性质, 不过并未使之成为完全可重整的理论。 但它距离将引力归入可重整量子场论的梦想又近了一步。 我们与超对称的所有互动都围绕着微扰量子场论的重整化问题。 必须被重整的奇异性是量子场论中不令人满意的短距离行为的结果。 对称性在一定程度上改善了局面。 但这果真是大自然解决短距离发散问题的方法吗? 另一种可能性是放宽某些公理。 但这必须以一种有受到很好控制的方式去做, 以便首先避免与实验事实相矛盾, 其次避免让理论游戏的规则过于开放, 以至于使理论变成一种簿记的工具。 迄今唯一满足这些条件的方法是弦论。 点的概念换成了弦的概念 - 局域性公理被放宽, 粒子的数目变为无穷, 它们是理论中弦的激发态。 在低能下, 弦图像也许能与我们用标准模型及 Einstein 引力理论所概括的实验知识相容。 弦的理论框架仍然是基于对称性与微分几何。 解析性也扮演着重要角色。 在弦论中, 我们关于时空的概念是建立在微分流形基础上的 - 它们无论多么弯曲, 都是与平直空间最相近的亲戚。 我们也可以寻求对量子场论代数结构的变更。 我们曾将之建立在量子力学的正则结构之上, 并改用到微分流形的代数可能性上。 非对易微分几何也许能提供一个超越微分流形的数学框架。 沿这一方向的努力表明, 它有可能导致短距离上的时空格点化。 这开启了值得探索的可能性。 二零零九年七月五日译于纽约
| 



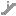

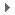
 收藏
收藏 转播
转播 分享
分享 淘帖
淘帖 支持
支持 反对
反对 楼主
楼主








